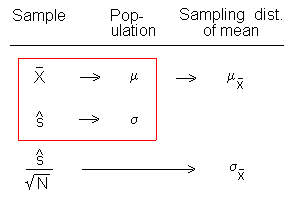
Because the mean of the sampling distribution of sample means is equal to the mean of the population, the sample mean is an unbiased estimator of the population mean, mu. Similarly, the mean of the sampling distribution of s-hat can be shown to equal the standard deviation of the population. Hence, s-hat is an unbiased estimator of the population standard deviation, sigma. These sample statistics and the population parameters they estimate are shown in the red box in the figure above.
Because of the relationship between the moments of the sampling distribution of the mean and the moments of the population distribution, the sample mean also estimates the mean of the sampling distribution of the mean, as indicated in the first line of the figure above. For the same reason, s-hat divided by the square root of N estimates the standard deviation of the sampling distribution of the mean, as indicated in the bottom line of the figure.
Back to Annotated Lecture Material and Supplementary Material.