Sampling distribution of the mean

samples of size, N, are drawn from a population with mean, mu, and standard deviation, sigma, and
the means of the samples are calculated, and
a frequency distribution of the means is prepared,

then this distribution is called the sampling distribution of the mean. The standard deviation, sigma-sub-X-bar, of this distribution is often called the standard error of the mean. The parameters of the sampling distribution of the mean are related to the parameters of the population, and to the size, N, of the samples drawn from the population, as indicated by the equations in the figure above. These relationships will be demonstrated analytically in class. Don't miss it!

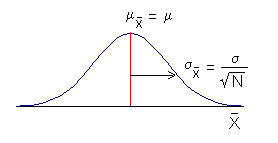
The sampling distribution of the mean describes how the sample means vary. Notice that the standard deviation of this distribution is directly related to the standard deviation of the population and is inversely related to the size of the samples drawn from the population. In other words, as the population standard deviation increases, so does the standard deviation of the sampling distribution of the mean. But as the size of the samples drawn from the population increases, the standard deviation of the sampling distribution of the mean decreases. Obviously, the smaller the standard deviation of the sampling distribution of the mean, the smaller the variability of the sample means.

Another, very important, property of the sampling distribution of the mean is that its form approaches the gaussian as N increases. This is true regardless of the form of the population distribution from which the samples are drawn. The gaussian form of the sampling distribution of the mean makes this distribution especially useful in calculating the probabilities of outcomes of experiments under the null hypothesis.

Back to Annotated Lecture Material and Supplementary Material.