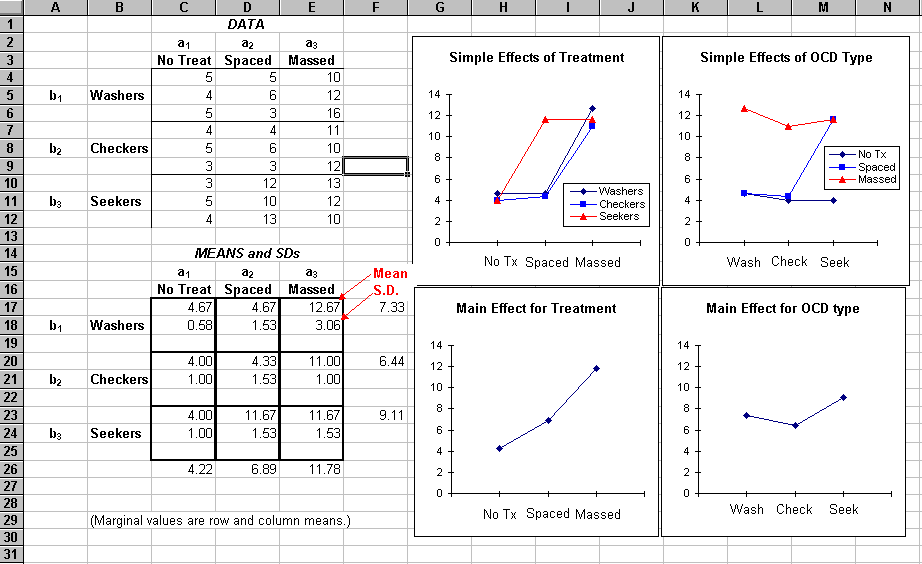
This is the example we have been working on in class. You should probably expand your browser to full screen.

The Brown-Forsythe test for homogeneity of variance:
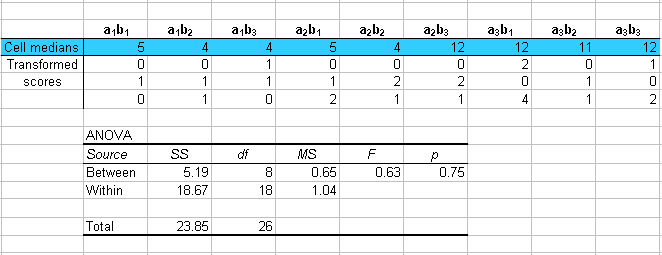
The omnibus ANOVA:

Analytic Comparisons
Because the interaction is significant, we test the simple effects:
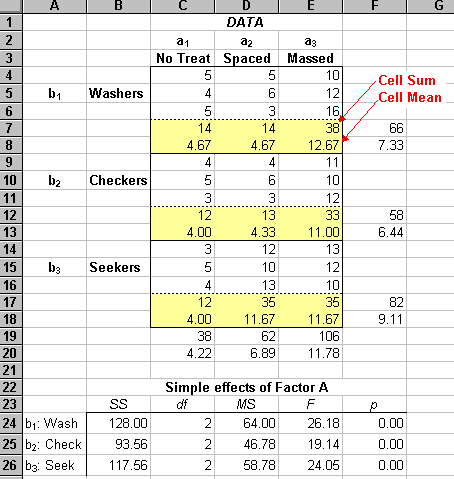
These effects can also be tested in SPSS. All the simple effects are significant, so we do some comparisons to pinpoint the source of the significant Fs:
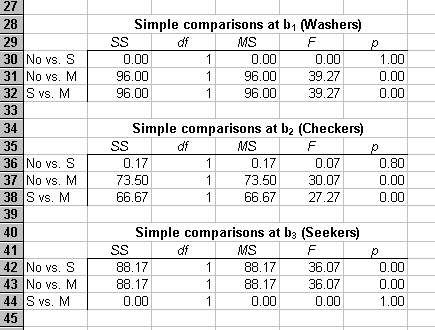
These comparisons show that the Washers and Checkers have the same outcome: massed ERP (exposure with response prevention) is better than both no treatment and spaced ERP, and spaced ERP is the same as no treatment. The Seekers are different: both massed and spaced ERP are better than no treatment, and they are not different from each other. In summary, massed ERP works for everybody. For the Seekers, spaced ERP works as well as massed ERP but for the Washers and Checkers, spaced ERP doesn't work at all.
Another approach to analyzing the interaction is to calculate partial interactions and interaction contrasts. The following is an example of calculating partial interactions.
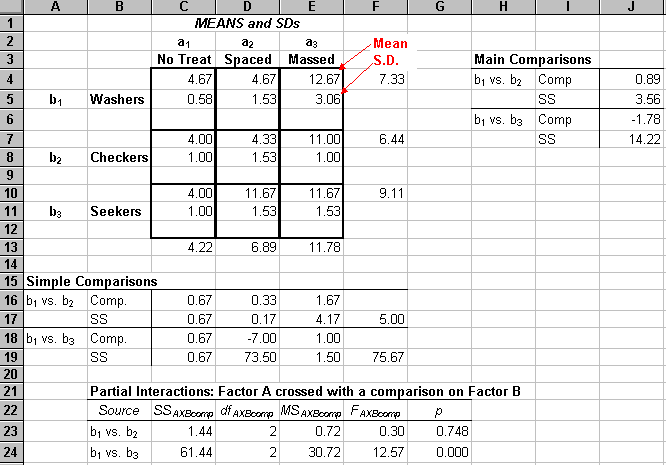
The first partial interaction crosses Factor A with levels 1 and 2 of Factor B. There is no partial interaction here, i.e., Washers and Checkers respond identically to the levels of Factor A. The second partial interaction crosses Factor A with levels 1 and 3 of Factor B. Here there is an interaction. Washers and Seekers respond differently to the levels of Factor A.
Interaction contrasts may also be illuminating. The following is an example of calculating interaction contrasts.
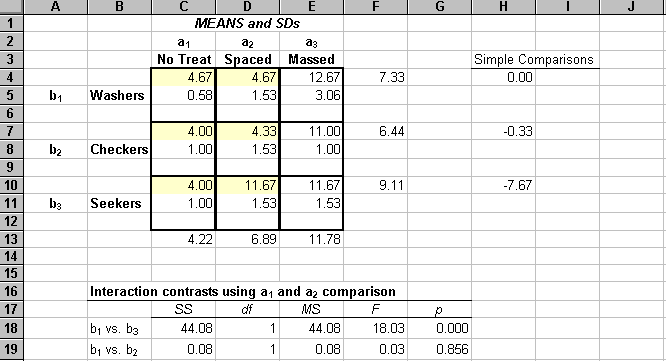
The first interaction contrast compares levels 1 and 2 of Factor A with levels 1 and 3 of Factor B. The significant F indicates that Washers and Seekers respond differently at the two levels of Factor A. The second interaction contrast compares levels 1 and 2 of Factor A with levels 1 and 2 of Factor B. The non-significant F indicates that Washers and Checkers respond identically at the two levels of Factor A.
Click your browser's back button to return to the factorial ANOVA page.