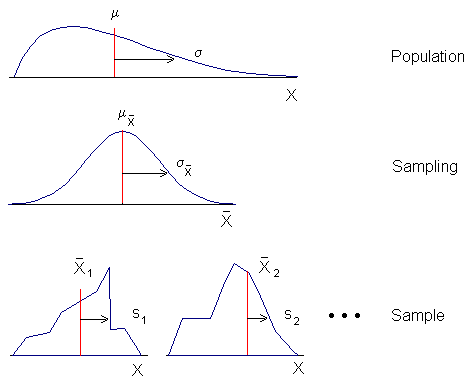
If samples are drawn from the population with replacement, then any number of samples of a given size, N, can be drawn. The moments of these samples themselves form distributions. Consider, for example, the means of the samples drawn from the population. One could prepare a frequency distribution of these means. A distribution of a sample statistic is referred to as a sampling distribution of that statistic. The middle distribution in the figure above is the sampling distribution of the mean. It is possible to prepare a sampling distribution of any statistic that can be calculated from sample data. For example, one could prepare a sampling distribution of the sample standard deviations.
Sampling distributions are important because they can be used to calculate the probabilities of experimental outcomes under the null hypothesis.
Back to Annotated Lecture Material and Supplementary Material.