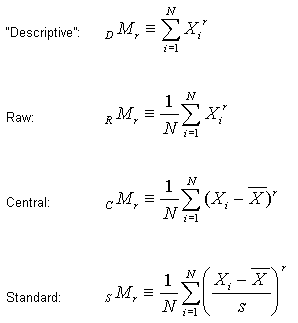
Statistical Moments
A frequency distribution can be described by its statistical moments. The definitions of the four types of moments are given below. Notice that, except for the "descriptive" moments, every summation is divided by N, the number of elements in the distribution. The raw, central, and standard moments take their names from the exponentiated quantities that appear in the summations. These quantities are referred to as raw, central, and standard (or z) scores in the corresponding moments.
The most interesting moments are the zeroth descriptive moment,
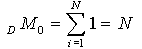 ,
,
which is the number of elements in the distribution, the first raw moment,
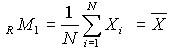 ,
,
which is the arithmetic mean of the distribution, the second central moment,
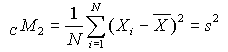 ,
,
which is the variance of the distribution, the third standard moment,
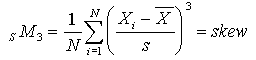 ,
,
which is the skew of the distribution, and the fourth standard moment,
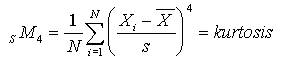 ,
,
which is the kurtosis of the distribution. Notice that the definition of each moment incorporates the most interesting of the lower-order moments. Thus, the definition of the raw moments entails N, the definition of the central moments entails N and the arithmetic mean, and the definition of the standard momements entails N, the arithmetic mean, and the positive square root of the variance.
 Back to Annotated Lecture Material and Supplementary Material.
Back to Annotated Lecture Material and Supplementary Material.


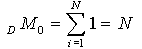 ,
,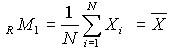 ,
,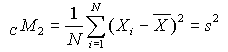 ,
,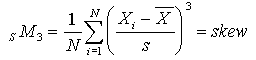 ,
,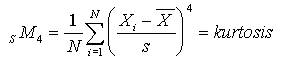 ,
, Back to Annotated Lecture Material and Supplementary Material.
Back to Annotated Lecture Material and Supplementary Material.